位并行算法与shift-and、shift-or算法

2011-11-17 3 条评论 13,534 次阅读 被赞了 1 次
目录
[隐藏]

一、关于位并行算法

二十世纪90年代初，在Baez-aYates的博士论文11”[1]中最早出现了采用位并行方法(Bit一Parallelism)进行字符串匹配的思想，而后出现了经典的shift-or算法，以及又在此基础上进行了改进和提高的shift-and算法[2]，shift-and算法又称为BAP(Bit一ParallelAutomaton)算法。

       位并行算法用来模拟经典算法，是一种加速算法实现的手段。在搜索中，通过并行模拟，可以加快经典算法的运行速度。位并行算法非常适合模式串比较短的情况。

位并行利用了计算机机器字位运算的内在并行性，可以把多个值装入同一个长度为w的机器字内，然后只需一次运算就能更新所有值。利用位并行，一个算法所执行的运算次数最多能减少到原来的1/W，这里W是机器字的位数。

二、Shift-and算法

Shift-And算法是一种基于前缀的单字符串匹配算法，采用位运算。其算法思想比KMP简单得多。

在最简单的brute force算法中，在文本串的每个位置都要进行m(模式串长度)次比较，而SHIFT AND算法则是利用位运算提高这个过程。现在计算机的字长一般为32，64位也开始流行了。一次比较的值为true or false，只需要一位即可存储，所以计算机可以在一次运算里完成 位长 次的比较。通过此思路可以把brute force的速度提高 位长 倍。

2.1 算法思想

Shift-And算法思想：设模式字符串为P，文本为text。它主要通过维护一个字符串集合D（D中记录了P中所有与当前已读text的某个后缀相匹配的前缀），集合D中的每个字符串既是模式串p的前缀，同时也是已读入文本的后缀，每当从text中读入一个新的字符，算法立即利用位并行机制来更新集合D。[3]

 我们可以这么具体理解：

  •  设P长度为m，则集合D可表示为D = dm…d1 而用D[j]代表dj；
  • D[j]=1，当且仅当p1…pj 是 t1…ti 的某个后缀；
  • 当D[m]=1时，就认为P已经于text匹配；
  • 当读入下一个字符 ti+1, 需要计算新的集合 D′；
  • 当且仅当D[j]=1并且  ti+1等于pj+1时D'[j+1]=1。这是因为D[j]=1时有 p1…pj是 t1…ti 的一个后缀，而当ti+1 等于 pj+1可推出p1…pj +1是 t1…ti+1 的一个后缀。这个集合可通过位运算来更新。

Shift-and算法首先建立一个数组B, 数组长度为字符集长度（例如A-Z的话数组B的长度为26），如果P的第j位等于c(P[j]=c)，则将B中第j位置为1，否则为0。

首先D=0m，对于每个新读入的文本字符ti+1，可以用如下公式对D进行更新：

公式(1)：D’  ß ((D << 1) | 0m-11) & B[ti+1]       (1)

直观上来讲，左移位操作<<将D’的第i+1位的值置为D的第i位。因为空字符串也是文本的后缀，所以D<<1需要在最低位与0m-11进行位或操作。因为要找到那些满足ti+1=pm+1的位置，所以需要再讲上面的结果与B[ti+1]进行位与操作。

当模式串的长度不超过几个机器字长时，公式(1)中的操作能够在常数时间内完成，这是shift-and算法的时间复杂度为O(n)。[2]

举例说明：

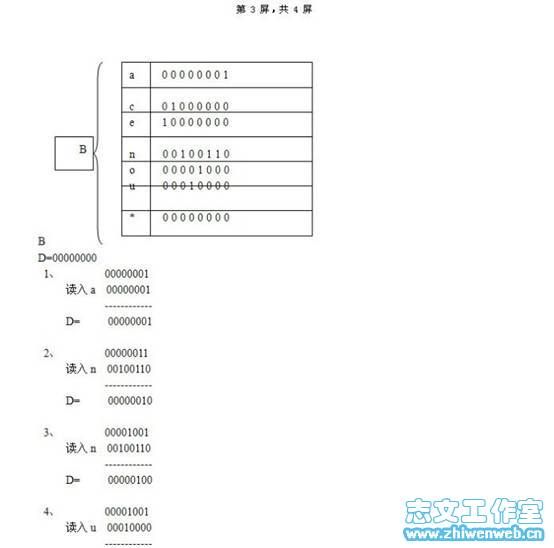
假如P=announce，则构建b[]的过程：

B[a]=1; b[n]=10; b[n]=110; b[o]=1000; b=10000; b[n]=100110; b=1000000; b[e]=10000000;

初始状态：D=00000000；

读入字符，通过公式(1)更改D结果。于是，D的每个时刻代表的字符集合，都是p的前缀，同时是已匹配文本的后缀。匹配过程如图2示例。

Shift-And算法
图1 匹配示例

因为要预处理计算B，如果字符集很大的话，并不划算。如果m很长的话（大于机器字长），也很不方便。所以这种算法适用于字符集较小，模式串小于机器字长的情况。当然对于模式串较长的情况，也是比brute force要快的，只是逻辑上要复杂些。

2.2 Shift-And算法示例

Shift-And算法示例代码如下，这里假设字符集的大小为128

XML/HTML代码
  1. int shift_and(char * s, int len_s, char * p, int len_p)   
  2. {   
  3.     int B[128];   
  4.     memset(B, 0, sizeof(B));   
  5.     int i;   
  6.     for (i=0; i<len_p; i++)   
  7.         B[p] |= 1<<i;   
  8.     int D = 0;   
  9.     for (i=0; i<len_s; i++)   
  10.     {   
  11.         D = ((D<<1) | 1) & B[s];   
  12.         if (D & (1<<(len_p-1)))   
  13.         return i – len_p+1;   
  14.     }   
  15.     return -1;   
  16. }  

三、关于shift-or算法

Shift-Or算法是Shift-And的一种技巧性的改进实现，其算法思想跟Shift-And类似，只是在通过对位取反以去掉公式中的掩码0m-11，这样减少了位运算的次数，从而实现加速。Shift-Or作的修改是，使用反码表示B中的位掩码和位向量，即用0表示一个数在集合里，1表示不在，所以将

D = ((D<<1) | 1) & B[s];

修改为

D=D<<1 | B[s];

这样就省了一次位运算，当然B和D的初始化的时候，也要作相应的修改。

3.1 一个shift-or算法示例程序

C++代码
  1. // 位并行算法Shift-Or算法   
  2. // 1、对模式串构造掩码表设模式串为abacb   
  3. //   a b a c b的掩码表为   
  4. // a 1 0 1 0 0   
  5. // b 0 1 0 0 1   
  6. // c 0 0 0 1 0   
  7. // 2、置D = 0， 对于新输入文本字符szMsg[j],   
  8. // 用公式D >> 1 | 2^(len-1) & Bset[Index]-> D   
  9. // if szMsg[j] = a or A Then Index = 0 Bset[Index] = 20   
  10. // 3、如果D&1==1当前的模式串与文本的以j个为结尾   
  11. // 的最后len个字符匹配.str[0]…str[len-1] = szMsg[j-len+1]..szMsg[j]   
  12.   
  13. #include <stdio.h>   
  14. #include <string.h>   
  15. #include <math.h>   
  16. const int MAX_LEN = 256;   
  17. // 创建位掩码集合   
  18. void CreateBset(char *str, int Bset[])   
  19. {   
  20.     int len = strlen(str);   
  21.     int i;   
  22.     int j;   
  23.     for (i=0; i<26; i++)// 行26 a到z   
  24.     {   
  25.          
  26.         for (j=0; j<len; j++)   
  27.         {   
  28.             if (i == (str[j] – 'A')%32)//大小写一样匹配字母对应数字映射   
  29.             {   
  30.                 Bset += (int)pow((double)2, (double)(len-1-j)); //出现的就是1   
  31.             }   
  32.         }   
  33.     }   
  34. return;   
  35. }   
  36. int main()   
  37. {   
  38.     char str[256] = {0};   
  39.     char szMsg[1024] = {0};   
  40.     //输入模式串   
  41.     gets(str);   
  42.     //输入文本   
  43.     gets(szMsg);   
  44.     int len = strlen(str);   
  45.     int Bset[26] = {0};   
  46.     int D = 0;//位掩码   
  47.     int Index;   
  48.     //创建掩码表集合   
  49.     CreateBset(str, Bset);   
  50.     int j = 0;   
  51.     int count = 0;   
  52.     while(j<strlen(szMsg))   
  53.     {   
  54.         D = (D >> 1) | (int)pow((double)2, (double)(len – 1));//右移1或上最高位为1   
  55.         Index = szMsg[j] – 'A';   
  56.         D = D & Bset[Index%32];//读入的文本的掩码集&上D   
  57.         if (1 == (D&1))//如果D的二进制第一位为1目标匹配   
  58.         {   
  59.             count++;//匹配的个数   
  60.         }   
  61.         j++;   
  62.     }   
  63.     printf("匹配的个数%dn", count);   
  64.     return 0;   
  65. }  

四、分析

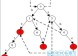
Shift-and和shift-or算法可看做是使用一个非确定性自动机对扫描文本的过程进行模拟。我们参考示例图2和图3进行分析，公式（1）对应于读入每个新字符时自动机的状态转移可如此来看：当文本字符与相应的箭头匹配时，当前状态转移到下一个状态。


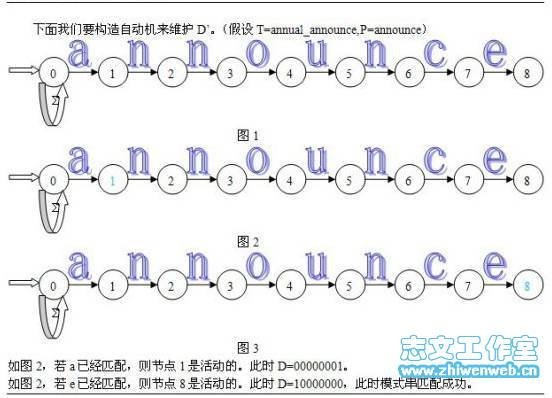
图2 自动机模拟匹配示意图

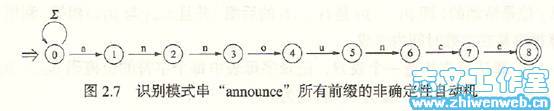
图3 非确定性自动机模拟

参考文献

 

[1] R.A. Baeza-Yates. Efficient Text Searching. PhD thesis, Dept. of Computer Science, University of Waterloo, May 1989. Also as Research Report CS-89-17.

[2] S.WU，U.Mnab.erFast text searhing allowing errors. Communieations of the ACM 1992，3510:83- 91.

[3] G. Navarro and M. Raffinot. Flexible Pattern Matching in Strings:Practical on-line search algorithms for texts and biological sequence[M].Cambridge: Cambridge University Press, 2002.

 

相关文章:

Default ThumbnailWM(Wu-Manber)算法详解及C语言实现程序代码解析参考 Default ThumbnailKMP（Knuth-Morris-Pratt）字符串模式匹配算法解析及C语言实现参考源码 Default Thumbnail常见经典字符串匹配算法简要介绍 & 柔性的字符串匹配pdf下载地址 Default Thumbnail精确单字符串匹配BM算法及其在snort中的C语言实现代码解析 Default Thumbnail计算机图形学裁剪：关于梁友栋-Barsky算法(Liang-Barsky算法) Default Thumbnail搜索引擎算法139个相关因素 Default Thumbnail卡巴斯基2009、2010、2011激活码授权文件key下载 Default Thumbnaillinux下的iscsi+lvm+raid配置详细步骤讲解 Default ThumbnailLinux CDP（连续性数据保护）实现方案、技术细节介绍及相关源码文档下载 Default Thumbnaillinux/ubuntu下的redis及PHP扩展phpredis安装与配置详细步骤参考
点赞 (1)
知识共享许可协议
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可
  1. 情侣对戒说道：
    2011年11月18日 1:16 上午

    好文章啊，就是看不懂

    回复
  2. 滨州楼盘出售说道：
    2011年11月17日 6:03 下午

    博主真是专业啊

    回复
  3. 潮人蛤蟆镜说道：
    2011年11月17日 11:50 上午

    我猛点进来 沙发真的是我的了

    回复

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注

Captcha Code